Ngtjyty

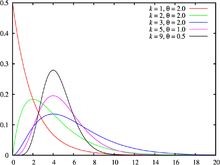
Distribució gamma.

En la teoria de la probabilitat i l'estadística, la distribució gamma és una
família de distribucions contínues amb dos paràmetres.
Té un paràmetre d'escala θ i un paràmetre de forma k. Si k
és un nombre sencer aleshores la distribució representa la suma de k variables aleatòries exponencials,
cadascuna de les quals té mitjana θ.

Caracterització

Una variable aleatòria gamma X amb escala θ i forma k es denota

X∼Γ(k,θ)orX∼Gamma(k,θ){displaystyle Xsim Gamma (k,theta ),,mathrm {or} ,,Xsim {textrm {Gamma}}(k,theta )}

Funció de densitat de probabilitat

La funció de probabilitat de densitat de la distribució gamma
pot expressar-se en termes de la funció gamma:

f(x;k,θ)=xk−1e−x/θθkΓ(k) for x>0andk,θ>0.{displaystyle f(x;k,theta )=x^{k-1}{frac {e^{-x/theta }}{theta ^{k},Gamma (k)}} mathrm {for} x>0,,mathrm {and} ,,k,theta >0.}

En aquesta parametrització l'esperança és
k/θ{displaystyle k/theta }
Alternativament, la distribució gamma pot parameteritzar-se en termes d'un
paràmetre de forma α=k{displaystyle alpha =k} i un paràmetre d'escala inversa
β=1/θ{displaystyle beta =1/theta }, anomenat un paràmetre de tasa:

g(x;α,β)=xα−1βαe−βxΓ(α) for x>0.{displaystyle g(x;alpha ,beta )=x^{alpha -1}{frac {beta ^{alpha },e^{-beta ,x}}{Gamma (alpha )}} mathrm {for} x>0,!.}

En la segona parametrització l'esperança és kθ{displaystyle ktheta }.
Ambdues parametritzacions són comunes perquè qualsevol de les dues pot
ésser més convenient depenent de la tasca a la que un s'enfronta.
És possible una tercera parametrització, on es manté el paràmetre
de forma α=k{displaystyle alpha =k} i s'introdueix l'esperança
μ=α/θ{displaystyle mu =alpha /theta }.
L'avantatge d'aquesta darrera parametrització és que és més fàcilment interpretable.

Funció de distribució

La funció de distribució pot expressar-se en termes de la
funció gamma incomplerta,

F(x;k,θ)=∫0xf(u;k,θ)du=γ(k,x/θ)Γ(k){displaystyle F(x;k,theta )=int _{0}^{x}f(u;k,theta ),du={frac {gamma (k,x/theta )}{Gamma (k)}},!}

Propietats

Moments

• Mitjana = kθ{displaystyle ktheta ,!}
  


• Mediana = no hi ha una expressió simple


• Moda = (k−1)θ{displaystyle (k-1)theta ,!} per k≥1{displaystyle kgeq 1,!}, 0 altrament


• Variància = kθ2{displaystyle ktheta ^{2},!}
  


• Asimetria = 2k{displaystyle {frac {2}{sqrt {k}}},!}
  


• Curtosis = 6k{displaystyle {frac {6}{k}},!}
  


• Entropia = k+ln⁡θ+ln⁡Γ(k)+(1−k)ψ(k){displaystyle k+ln theta +ln Gamma (k)+(1-k)psi (k)!}
  


• Funció generadora de moments = (1−θt)−k{displaystyle (1-theta ,t)^{-k},!} for t<1/θ{displaystyle t<1/theta ,!}
  


• Funció característica = (1−θit)−k{displaystyle (1-theta ,i,t)^{-k},!}
  

Suma

Si X_i segueix una distribució Γ(α_i, β)
per a i = 1, 2, ..., N, aleshores

∑i=1NXi∼Γ(∑i=1Nαi,β){displaystyle sum _{i=1}^{N}X_{i}sim Gamma left(sum _{i=1}^{N}alpha _{i},beta right),!}

assumint que totes les X_i són independents.

La distribució gamma és infinitament divisible.

Transformació d'escala

Per a qualssevol t > 0 es compleix que tX segueix una distribució
Γ(k, tθ), demonstrant que θ és un paràmetre d'escala.

Família exponencial

La distribució gamma pertany a la família exponencial de
dos paràmetres
i té paràmetres naturals k−1{displaystyle k-1} i 1/θ{displaystyle 1/theta }, i estadístics naturals X{displaystyle X} i ln⁡(X){displaystyle ln(X)}.

Entropía

L'entropia ve donada per

−1θkΓ(k)∫0∞xk−1ex/θ[(k−1)ln⁡x−x/θ−kln⁡θ−ln⁡Γ(k)]dx{displaystyle {frac {-1}{theta ^{k}Gamma (k)}}int _{0}^{infty }{frac {x^{k-1}}{e^{x/theta }}}left[(k-1)ln x-x/theta -kln theta -ln Gamma (k)right],dx!}

=−[(k−1)(ln⁡θ+ψ(k))−k−kln⁡θ−ln⁡Γ(k)]{displaystyle =-left[(k-1)(ln theta +psi (k))-k-kln theta -ln Gamma (k)right]!}

=k+ln⁡θ+ln⁡Γ(k)+(1−k)ψ(k){displaystyle =k+ln theta +ln Gamma (k)+(1-k)psi (k)!}

on ψ(k) és la funció digamma.

Divergència Kullback-Leibler

La divergència Kullback-Leibler entre una Γ(α₀, β₀) (la distribució veritable) i una Γ(α, β) (la distribució que l'aproxima) ve donada per

DKL(α,β||α0,β0)=log⁡(Γ(α0)β0α0Γ(α)βα0)+(α−α0)ψ(α)+αβ−β0β0{displaystyle D_{mathrm {KL} }(alpha ,beta ||alpha _{0},beta _{0})=log left({frac {Gamma ({alpha _{0}})beta _{0}^{alpha _{0}}}{Gamma (alpha )beta ^{alpha _{0}}}}right)+(alpha -{alpha _{0}})psi (alpha )+alpha {frac {beta -beta _{0}}{beta _{0}}}}

Transformada de Laplace

La transformada de Laplace de la distribució gamma és:

F(s)=βα(s+β)α{displaystyle F(s)={frac {beta ^{alpha }}{(s+beta )^{alpha }}}}

Estimació dels paràmetres

Màxima versemblança

La funció de versemblança per a N observacions
iid
(x1,…,xN){displaystyle (x_{1},ldots ,x_{N})} és

L(θ)=∏i=1Nf(xi;k,θ){displaystyle L(theta )=prod _{i=1}^{N}f(x_{i};k,theta ),!}

de la qual podem calcular la log-versemblança

ℓ(θ)=(k−1)∑i=1Nln⁡(xi)−∑xi/θ−Nkln⁡(θ)−Nln⁡Γ(k).{displaystyle ell (theta )=(k-1)sum _{i=1}^{N}ln {(x_{i})}-sum x_{i}/theta -Nkln {(theta )}-Nln {Gamma (k)}.}

L'estimador màxim-versemblant s'obté maximitzant la log-versemblança,
és a dir, calculant-ne la derivada i igualant a zero (es pot demostrar
que la funció és convexa i que per tant té un sol extrem).
Procedint d'aquesta manera trobem que:

θ^=1kN∑i=1Nxi.{displaystyle {hat {theta }}={frac {1}{kN}}sum _{i=1}^{N}x_{i}.,!}

Substituint aquest resultat a l'expressió de la log-versemblança dóna

ℓ=(k−1)∑i=1Nln⁡(xi)−Nk−Nkln⁡(∑xikN)−Nln⁡(Γ(k)).{displaystyle ell =(k-1)sum _{i=1}^{N}ln {(x_{i})}-Nk-Nkln {left({frac {sum x_{i}}{kN}}right)}-Nln {(Gamma (k))}.,!}

Per trobar el màxim respecte de k cal calcular la derivada i
igualar-la a zero, amb què s'obté:

ln⁡(k)−ψ(k)=ln⁡(1N∑i=1Nxi)−1N∑i=1Nln⁡(xi){displaystyle ln {(k)}-psi (k)=ln {left({frac {1}{N}}sum _{i=1}^{N}x_{i}right)}-{frac {1}{N}}sum _{i=1}^{N}ln {(x_{i})},!}

on

ψ(k)=Γ′(k)Γ(k){displaystyle psi (k)={frac {Gamma '(k)}{Gamma (k)}}!}

és la funció digamma.
No existeix cap fórmula tancada per a k, però la funció es comporta bé
numèricament (és convex), i per tant és senzill trobar-ne una solució numèrica,
per exemple amb el mètode de Newton.
És possible trobar un valor inicial per a k
emprant el mètode dels moments,
o emprant l'aproximació

ln⁡(k)−ψ(k)≈1k(12+112k+2).{displaystyle ln(k)-psi (k)approx {frac {1}{k}}left({frac {1}{2}}+{frac {1}{12k+2}}right).,!}

Si definim

s=ln⁡(1N∑i=1Nxi)−1N∑i=1Nln⁡(xi),{displaystyle s=ln {left({frac {1}{N}}sum _{i=1}^{N}x_{i}right)}-{frac {1}{N}}sum _{i=1}^{N}ln {(x_{i})},,!}

aleshores k és aproximadament

k≈3−s+(s−3)2+24s12s{displaystyle kapprox {frac {3-s+{sqrt {(s-3)^{2}+24s}}}{12s}}}

que és dins d'un 1,5% del valor correcte.

Estimador Bayesià

Si considerem que k és conegut i θ{displaystyle theta } és
desconegut, la funció de densitat a posteriori per a θ{displaystyle theta } és
(assumint que la distribució a priori és proporcional a 1/θ{displaystyle 1/theta })

P(θ|k,x1,...,xN)∝1/θ∏i=1Nf(xi;k,θ).{displaystyle P(theta |k,x_{1},...,x_{N})propto 1/theta prod _{i=1}^{N}f(x_{i};k,theta ).,!}

Definint

y≡∑i=1Nxi,P(θ|k,x1,…,xN)=C(xi)θ−Nk−1e−y/θ.{displaystyle yequiv sum _{i=1}^{N}x_{i},qquad P(theta |k,x_{1},dots ,x_{N})=C(x_{i})theta ^{-Nk-1}e^{-y/theta }.!}

Per tal de calcular l'esperança cal calcular la integral respecte &theta,
el qual pot dur-se a terme emprant un canvi de variables que
revela que 1/&theta segueix una distribució gamma amb paràmetres
α=Nk,  β=y{displaystyle scriptstyle alpha =Nk, beta =y}.

∫0∞θ−Nk−1+me−y/θdθ=∫0∞xNk−1−me−xydx=y−(Nk−m)Γ(Nk−m).{displaystyle int _{0}^{infty }theta ^{-Nk-1+m}e^{-y/theta },dtheta =int _{0}^{infty }x^{Nk-1-m}e^{-xy},dx=y^{-(Nk-m)}Gamma (Nk-m).!}

Els moments podem calcular-se especificant diferents valors per a m a
la següent expressió

E(xm)=Γ(Nk−m)Γ(Nk)ym,{displaystyle E(x^{m})={frac {Gamma (Nk-m)}{Gamma (Nk)}}y^{m},!}

Per exemple, l'esperança +/- la desviació estàndard de la distribució
a posteriori de θ{displaystyle theta } és:

yNk−1{displaystyle {frac {y}{Nk-1}}} +/- y2(Nk−1)2(Nk−2).{displaystyle {frac {y^{2}}{(Nk-1)^{2}(Nk-2)}}.}

També és possible obtenir estimadors Bayesians sense assumir que k
és conegut, però en general no és possible obtenir-ne una expressió senzilla.

Generant valors d'una distribució gamma

Tenint en compte la propietat d'escala esmentada anteriorment,
és suficient generar una variable gamma amb β = 1
i després transformar-la a qualsevol altre valor de β
amb una simple divisió.

Emprant el fet que una distribució Γ(1, 1) és el mateix que una distribució exponencial Exp(1), i tenint en compte el mètode per generar variables aleatòries exponencials,
arribem a la conclusió de què si U prové d'una distribució uniforme en (0, 1],
aleshores -ln(U) segueix una Γ(1, 1).
Emprant la propietat de què la suma de variables aleatòries gamma independents
segueix novament una distribució gamma, extenem el resultat:

∑k=1n−ln⁡Uk∼Γ(n,1),{displaystyle sum _{k=1}^{n}{-ln U_{k}}sim Gamma (n,1),}

on U_k són uniformement distribuïdesen (0, 1] i independents.

Tanmateix aquesta estratègia només funciona si n és un nombre sencer.
Ara veurem com generar observacions d'una Γ(δ, 1) per a 0 < δ < 1,
ja que després podem aplicar la propietat de la suma per al cas 1 < &delta.

A continuació presenten un algoritme, sense demostració. Es tracta d'un cas particular del mètode d'acceptació-rebuig:

1. Sigui m= 1.


2. Generar V2m−1{displaystyle V_{2m-1}} i V2m{displaystyle V_{2m}} — independents i uniformement distribuïdes a (0, 1].


3. Si V2m−1≤v0{displaystyle V_{2m-1}leq v_{0}}, on v0=ee+δ{displaystyle v_{0}={frac {e}{e+delta }}}, aleshores anar a 4, altrament anar a 5.


4. Sigui ξm=V2m−11/δ, ηm=V2mξmδ−1{displaystyle xi _{m}=V_{2m-1}^{1/delta }, eta _{m}=V_{2m}xi _{m}^{delta -1}}. Anar a 6.


5. Sigui ξm=1−ln⁡V2m−1, ηm=V2me−ξm{displaystyle xi _{m}=1-ln {V_{2m-1}}, eta _{m}=V_{2m}e^{-xi _{m}}}.


6. Si ηm>ξmδ−1e−ξm{displaystyle eta _{m}>xi _{m}^{delta -1}e^{-xi _{m}}}, aleshores incrementar m i tornar a 2.


7. Assumim que ξ=ξm{displaystyle xi =xi _{m}} és l'observació d'una Γ(δ,1){displaystyle Gamma (delta ,1)}
   

Per resumir,

θ(ξ−∑i=1[k]ln⁡Ui)∼Γ(k,θ),{displaystyle theta left(xi -sum _{i=1}^{[k]}{ln U_{i}}right)sim Gamma (k,theta ),}

on
[k] és la part sencera de k, i ξ ha estat generat emprant l'algoritme que hem presentat δ = {k} (la part fraccional de k),
U_k i V_l segueixen la distribució explicada anteriorment i són independents.

La Llibreria científica GNU disposa de
rutines robustes per a generar observacions de moltes distribucions,
incloent la distribució Gamma.

Distribucions relacionades

Casos particulars

• Si X∼Γ(k=1,θ=1/λ){displaystyle Xsim {Gamma }(k=1,theta =1/lambda ),}, aleshores X segueix una distribució exponencial amb paràmetre λ.


• Si X∼Γ(k=v/2,θ=2){displaystyle Xsim {Gamma }(k=v/2,theta =2),}, aleshores X és idènticament distribuïda a una χ²(ν), la distribució khi-quadrat amb ν graus de llibertat.


• Si k{displaystyle k} és un nombre sencer, la distribució gamma es denomina

distribució d'Erlang que serveix per a modelar el temps d'arribada fins a la k{displaystyle k}-ena "arribada" en un procés de Poisson d'una dimensió amb intensitat 1/θ.

• Si X2∼Γ(3/2,2a2){displaystyle X^{2}sim {Gamma }(3/2,2a^{2}),}, aleshores X segueix una distribució de Maxwell-Boltzmann amb paràmetre a.


• 
  X∼SkewLogistic(θ){displaystyle Xsim mathrm {SkewLogistic} (theta ),}, aleshores log(1+e−X)∼Γ(1,θ){displaystyle mathrm {log} (1+e^{-X})sim Gamma (1,theta ),}
  

Altres

• Si X segueix una Γ(k, θ) aleshores 1/X segueix una distribució gamma inversa amb paràmetres k i θ^-1.


• Si X i Y són Γ(α, θ) i Γ(β, θ) independents, respectivament, aleshores X / (X + Y) segueix una distribució beta amb paràmetres α i β.


• Si X_i són Γ(α_i,θ) independents, aleshores el vector (X₁ / S, ..., X_n / S), on S = X₁ + ... + X_n, segueix una distribució de Dirichlet amb paràmetres α₁, ..., α_n.

Bibliografia

A Wikimedia Commons hi ha contingut multimèdia relatiu a: Distribució gamma

• R. V. Hogg and A. T. Craig. Introduction to Mathematical Statistics, 4th edition. New York: Macmillan, 1978. (See Section 3.3.)
  


• Weisstein, Eric W., «Gamma distribution» a MathWorld (en anglès).


• Engineering Statistics Handbook


• S. C. Choi and R. Wette. (1969) Maximum Likelihood Estimation of the Parameters of the Gamma Distribution and Their Bias, Technometrics, 11(4) 683-69