Ngtjyty

Distribució exponencial

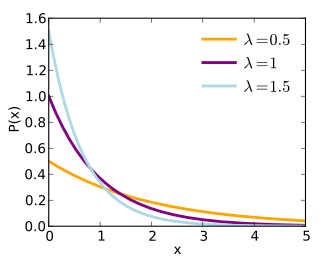Funció de distribució de probabilitat
Paràmetres	λ>0{displaystyle lambda >0,}
Suport	[0,∞){displaystyle [0,infty )!}
FD	1−e−λx{displaystyle 1-e^{-lambda x}}
Mitjana	1/λ{displaystyle 1/lambda ,}
Mediana	ln⁡(2)/λ{displaystyle ln(2)/lambda ,}
Moda	0{displaystyle 0,}
Variància	1/λ2{displaystyle 1/lambda ^{2},}
Coeficient de simetria	2{displaystyle 2,}
Curtosi	6{displaystyle 6,}
Entropia	1−ln⁡(λ){displaystyle 1-ln(lambda ),}
FGM	(1−tλ)−1{displaystyle left(1-{frac {t}{lambda }}right)^{-1},}
FC	(1−itλ)−1{displaystyle left(1-{frac {it}{lambda }}right)^{-1},}

A l'entorn d'estadística la distribució exponencial és una distribució de probabilitat contínua amb un paràmetre λ>0{displaystyle lambda >0} la funció de densitat és:

f(x)={λe−λx  per a x≥00  altrament{displaystyle f(x)=left{{begin{matrix}lambda e^{-lambda x}& {mbox{per a }}xgeq 0\0& {mbox{altrament}}end{matrix}}right.}

La seva funció de distribució és:
F(x)=P(X≤x)={0per a x<01−e−λxper a x≥0{displaystyle F(x)=P(Xleq x)=left{{begin{matrix}0&{mbox{per a }}x<0\1-e^{-lambda x}&{mbox{per a }}xgeq 0end{matrix}}right.}
on e{displaystyle e} representa el nombre e.

El valor esperat i la variància d'una variable aleatòria X amb distribució exponencial són:

• E[X]=1λ{displaystyle E[X]={frac {1}{lambda }}}


• V(X)=1λ2{displaystyle V(X)={frac {1}{lambda ^{2}}}}

Exemple

Exemples per a la distribució exponencial és la distribució de la longitud dels intervals de variable contínua que transcorre entre l'ocurrència de dos successos "rars", que es distribueixen segons la distribució de Poisson.

Calcular variables aleatòries

Es pot calcular una variable aleatòria de distribució exponencial x{displaystyle x} per mitjà d'una variable aleatòria de distribució uniforme u=U(0,1){displaystyle u=U(0,1)}:

x=−ln⁡uλ{displaystyle x=-{frac {ln u}{lambda }}}

Relacions

La suma de k{displaystyle k} variables aleatòries independents de distribució exponencial amb paràmetre λ{displaystyle lambda } és una variable aleatòria de distribució gamma.

Vegeu també

A Wikimedia Commons hi ha contingut multimèdia relatiu a: Distribució exponencial

• 
  Procés de Poisson.


• 
  Distribució de Poisson.