Freqüència
| Tipus | propietat física escalar i ISQ derived quantity |
|---|---|
| Símbol | f i ν |
| Fórmula | f=1T{displaystyle f={frac {1}{T}}} |

Modulació de freqüència
La freqüència és la mesura del nombre de vegades que ocorre un esdeveniment per unitat de temps. Per calcular la freqüència, es fixa un interval de temps, es compta el nombre de vegades que ocorre l'esdeveniment en eixe interval i aleshores es divideix aquesta quantitat per la llargària de l'interval de temps.
En mecànica quàntica, la freqüència d'oscil·lació de la funció d'ona d'estat representa l'energia d'aquest estat, i per tant hom escull sovint el sistema d'unitats de tal manera que la freqüència i l'energia s'expressin en les mateixes unitats. En altres paraules, el factor de conversió entre la freqüència i l'energia –la constant de Planck a l'equació E = hν– és igual a 1.

Tres llums intermitents de forma cíclica, amb freqüències (f) de 0,5 Hz (a dalt), 1 Hz (centre) i 2 Hz (a sota). El període (T), mostrat en segons, és recíproc a la freqüència.

Ones sinusoïdals de diferents freqüències. A la part superior, les de freqüència més baixa, i amb freqüència creixent segons baixem en el gràfic. L'eix horitzontal representa el temps.

Canvis de freqüència
Per als processos cíclics com són la rotació, l'oscil·lació o les ones la freqüència es defineix com el nombre de cicles o períodes per unitat de temps. A les disciplines de la física i l'enginyeria com l'òptica, l'acústica i la ràdio la freqüència es representa habitualment amb la lletra f o amb la lletra grega ν (ni).
En unitats del SI, el resultat es mesura en hertzs, anomenat així en honor del físic alemany Heinrich Rudolf Hertz. 1 Hz vol dir que un esdeveniment es repeteix una vegada cada segon, la unitat va ser coneguda originàriament com a cps o cicle per segon. Altres unitats que s'han usat per mesurar la freqüència són els cops per minut o batecs per minut (bpm) que s'utilitza per mesurar el tempo de la música (i el ritme del cor) o les revolucions per minut (rpm) en el cas de la freqüència de rotació. Tant els valors en bpm com en rpm poden ser convertits en hertz dividint per 60, 1 Hz equival a 60 rpm.
Un altre mètode alternatiu per calcular la freqüència és mesurar el temps entre dos esdeveniments consecutius (al que anomenem el període) i llavors calcular la freqüència com la inversa d'aquest temps:
- f=1T{displaystyle f={frac {1}{T}}}
on T és el període.
Al SI la unitat pel període és el segon.
Contingut
1 La freqüència a les ones
2 Període i freqüència
3 Freqüència de mostratge
4 Freqüència angular
5 Freqüència en la música
6 Freqüència en el llenguatge col·loquial
7 Freqüència en matemàtiques
7.1 En teoria de la probabilitat
7.2 En estadística matemàtica
8 Altres tipus de freqüència
9 Metrologia
9.1 Càlculs
9.2 Ús d'estroboscopis
9.3 Ús de freqüencímetres
9.4 Tècniques indirectes de mesurament
10 Visió intuïtiva
11 Exemples
11.1 Radiació electromagnètica
11.2 So
11.3 Electricitat
12 Freqüències especials
13 Rangs de freqüències
14 Referències
15 Bibliografia
16 Vegeu també
La freqüència a les ones
La freqüència està relacionada amb la longitud d'ona, la freqüència és inversament proporcional a la longitud d'ona λ (lambda). Dit d'una altra manera, la freqüència f és igual a la velocitat de fase v de l'ona dividida per la longitud d'ona λ.
- f=vλ.{displaystyle f={frac {v}{lambda }}.}
En el cas especial de les ones electromagnètiques que viatgen al buit, v = c, on c és la velocitat de la llum al buit, i l'expressió anterior esdevindrà:
- f=cλ{displaystyle f={frac {c}{lambda }}}
Quan les ones d'una font de llum monocroma travessen d'un medi òptic vers un altre, la seva freqüència continua essent la mateixa, l'únic que canvia és la seva longitud d'ona i la seva velocitat de fase. A part que pot variar per l'efecte doppler, la freqüència és una magnitud invariable a tot l'univers. És a dir, no es pot modificar per cap procés físic excepte per la seva velocitat de propagació o longitud d'ona.
Període i freqüència
Per una qüestió de conveniència, les ones més llargues i lentes, com les onades del mar, tendeixen a ser descrites a partir del període en comptes de la freqüència. Per contra, les ones més curtes, com les sonores o les de ràdio (l'espectre radioelèctric), acostumen a ser descrites basant-se en la seva freqüència. Aquestes convencions es mostren a la següent taula:
| Freqüència (hertz) | 1 mHz (10-3) | 1 Hz (100) | 1 kHz (103) | 1 MHz (106) | 1 GHz (109) | 1 THz (1012) |
|---|---|---|---|---|---|---|
| Període (segons) | 1 ks (103) | 1 s (100) | 1 ms (10-3) | 1 µs (10-6) | 1 ns (10-9) | 1 ps (10-12) |
Freqüència de mostratge
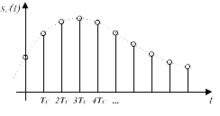
Mostratge d'un senyal analògic
La freqüència de mostratge és un dels paràmetres bàsics que caracteritzen el procés de conversió analògic-digital als sistemes electrònics de processament d'informació.En un sistema electrònic, la informació acostuma a ser codificada en un senyal elèctric que varia el seu voltatge amb el temps. Parlem de senyal analògic si varia contínuament moment del temps, i de senyal digital si només presenta un nombre finit de valors discrets al llarga del temps. El procés de mostreig consisteix a convertir un senyal analògic en un senyal digital mesurant i enregistrant, en moments específics del temps (instants de mostra), el valor instantani del senyal analògic. La seqüència d'aquests valors, les mostres preses, és el senyal digital. El dispositiu realitza la conversió d'analògic a digital del senyal és un convertidor analògic-digital. La freqüència de mostratge és el nombre de mostres enregistrades en un segon: el Teorema de mostreig de Nyquist-Shannon, estableix que, perquè puguem reconstruir el senyal analògic a partir de les mostres, cal que la freqüència de mostratge sigui com a mínim el doble de la freqüència més alta del senyal analògic que s'intenta digitalitzar:fm>=2fmax{displaystyle f_{m}>=2f_{max}}.
Freqüència angular
En electrodinàmica clàssica, en la física teòrica i en algunes aplicacions és convenient utilitzar un concepte addicional, la freqüència angular. És una quantitat física escalar que mesura la freqüència del moviment de vibració o rotació. En el cas del moviment de rotació, la freqüència angular és igual al mòdul de la velocitat angular. Al SI i al CGS, es mesura en radians per segon, i la seva magnitud és la de l'invers del temps (els radians són adimensionals). La relació entre la freqüència angular ω i la freqüència f és: ω = 2πf.
En el cas que mesurem els angles en graus, la relació és ω = 360°·f.
Numèricament, la freqüència angular representa el nombre de cicles (o vibracions, o rotacions) per cada 2π segons. La introducció del concepte de freqüència angular (en la seva dimensió bàsica, radians per segon) permet simplificar moltes de les fórmules de la física teòrica i l'electrònica. Així, la freqüència angular de la ressonància d'un circuit LC és ωLC=1/LC{displaystyle omega _{LC}=1/{sqrt {LC}}}, mentre que la freqüència ordinària de ressonància és fLC=1/(2πLC){displaystyle f_{LC}=1/(2pi {sqrt {LC}})}. L'aspecte a favor de la freqüència angular és que els factors 2π i 1 / (2π), que apareixen en moltes de les fórmules (quan s'utilitzen els radians com a unitat de mesura d'angles), desapareixen amb la introducció de la freqüència angular.
Freqüència en la música
En música, els sons audibles es caracteritzen per una quantitat fisiològica: l'altura, que és, senzillament, la freqüència fonamental del corresponent so. L'altura també s'expressa en Hertz (Hz). L'espectre de freqüències audibles per l'oïda humana s'estén des dels 20 Hz als 20000 Hz aproximadament.
Per convenció, s'ha escollit la freqüència de 440 Hz com la freqüència de referència per afinar els instruments musicals. El motiu és que aquesta és la freqüència de la nota La3: la nota musical "La" en la tercera octava.
Des del punt de vista matemàtic, és possible realitzar diversos càlculs entre les notes musicals i les seves freqüències. Si dupliquem una freqüència obtenim una octava, mentre que si sumem una freqüència i la de la seva octava inferior obtenim una quinta. Aleshores, la suma de dues octaves inferiors ens dóna una tercera major. Per exemple:
| Freqüència | Nota | Interval | Càlcul |
|---|---|---|---|
| 110 | La1 | Octava | 440/4 |
| 220 | La2 | Octava | 440/2 |
| 440 | La3 | Octava | (referència) |
| 550 | Do# | Tercera Major | 440 + 110 |
| 660 | Mi | Quinta justa | 440 + 220 |
| 990 | Si | Quinta justa (Mi-Si) | 660 + 330 |
Tot i això, hem de considerar que aquests intervals són purs i no-temperats.
Freqüència en el llenguatge col·loquial
En el llenguatge col·loquial, hom utilitza de vegades el terme freqüència de forma incorrecta. Per exemple, a la frase "la freqüència de pas dels autobusos ha augmentat, ara n'hi ha un cada 10 minuts", el que es menciona és el valor del període, i no pas la freqüència. Tot i això, cal remarcar que la freqüència ha augmentat perquè el període temporal (en aquest cas, el temps entre el pas entre dos autobusos) ha disminuït.
Freqüència en matemàtiques
En teoria de la probabilitat
En el marc de la teoria de la probabilitat la freqüència relativa d'un esdeveniment és un dels conceptes fonamentals, juntament amb la probabilitat real. Terminològicament es defineix com la relació entre el nombre de mostres que acompleixen un cert esdeveniment, respecte al nombre total de mostres realitzades. La freqüència relativa de l'esdeveniment pot ser calculada només després del mostreig. La freqüència relativa es caracteritza per l'estabilitat: d'acord amb els resultats de les observacions, per a un nombre prou gran d'experiments duts a terme en condicions idèntiques, l'indicador no canvia i fluctua al voltant d'una certa constant.[1]
En estadística matemàtica

Exemple: variables de A en una mostra estadística d'un conjunt B de dimensió 50 (N).
En estadística es poden distingir fins a quatre tipus de freqüències:
Freqüència absoluta És la mitjana d'una suma predeterminada i, a més, consisteix a saber quin es el nombre o símbol d'equivalència més gran. (ni) d'una variable estadística Xi, és el nombre de vegades que aquest valor apareix a l'estudi. Com més gran és la mostra, més augmentarà el valor de la freqüència absoluta; és a dir, la suma total de totes les freqüències absolutes ha de donar el total de la mostra estudiada (N).
Freqüència relativa (fi), és el quocient entre la freqüència absoluta i la mida de la mostra (N). És a dir,
- fi=niN=ni∑ini{displaystyle f_{i}={frac {n_{i}}{N}}={frac {n_{i}}{sum _{i}n_{i}}}}
- essent els fi per a tot el conjunt de valors i. Es presenta en una taula o núvol de punts en una distribució de freqüències.
- Si multipliquem la freqüència relativa per 100 s'obté el percentatge (pi)
Freqüència absoluta acumulada (Ni), és el nombre de vegades ni a la mostra N.
Freqüència relativa acumulada (Fi), és el quocient entre la freqüència absoluta acumulada Ni respecte a la mostra N
- Fi=NiN{displaystyle F_{i}={frac {N_{i}}{N}}}
Altres tipus de freqüència
Freqüència angular (simbolitzada com ω), es defineix com la variació de l'angle o la posició angular al llarg del temps en els moviments de rotació o en la fase de les ones de forma sinusoïdal. La freqüència angular es mesura en radiants per segon (rad/s) i es defineix com:
- ω=2πf{displaystyle omega =2pi f,}
| Demostració |
|---|
Si la funció d'ona és
llavors la seva taxa de canvi és
|
- Per senyals discrets també es pot expressar com a radians per temps mostral, que és una magnitud adimensional.
Freqüència espacial és el nombre de cicles per unitat de longitud donada una direcció. Al Sistema Internacional es mesura en cicles per metre. És l'anàloga a la freqüència temporal, però en aquest cas se substitueix l'eix temporal per un o més eixos de desplaçament espacial. Per exemple:
- y(t)=sin(θ(t,x))=sin(ωt+kx){displaystyle y(t)=sin left(theta (t,x)right)=sin(omega t+kx),}
- dθdx=k.{displaystyle {frac {dtheta }{dx}}=k.,}
Nombre d'ona és una magnitud proporcional al nombre d'oscil·lacions per unitat de longitud, el nombre de longituds d'ona que hauria en una distància de 2π unitats de longitud. Al SI es mesura en radians/metre (rad/m), i s'obté de la relació:
- k=2πλ{displaystyle k={frac {2pi }{lambda }}}
- En el cas multidimensional, el nombre d'ona és un vector.
Metrologia
Per mesurar la freqüència es fan servir freqüencímetres de diferents tipus, incloent: per mesurar la freqüència del pols - amb electrons i condensador, per determinar les freqüències dels components espectrals -, ressonància, comptadors de freqüència heterodí i analitzadors d'espectre. Per reproduir una freqüència determinada amb precisió utilitzant diferents mesures (patrons de freqüència d'alta precisió), sintetitzadors de freqüència, generadors de senyals, etc. Es poden comparar les mesures amb un comparador de freqüència o utilitzar un oscil·loscopi fent servir la corba de Lissajous.
Càlculs
El càlcul de la freqüència de l'esdeveniment es porta a terme comptant el nombre d'ocurrències de l'esdeveniment en un termini determinat de temps. El nombre resultant es divideix per la longitud de l'interval de temps corresponent. Per exemple, si en un període de 15 segons s'obté una mesura homogènia de 71 esdeveniments, la freqüència serà:
- f=7115s≈4.7Hz{displaystyle f={frac {71}{15,{mbox{s}}}}approx 4.7,{mbox{Hz}},}
Si el nombre de mostres és petit, una tècnica més precisa és mesurar l'interval de temps per a un nombre predeterminat d'ocurrències de l'esdeveniment, i no trobar el nombre d'esdeveniments dins d'un període predeterminat.[2]
Utilitzant aquest últim mètode s'introdueix entre el zero i la primera lectura aleatòria d'error mitjanes marc, i això pot donar lloc a errors a la freqüència mitjana calculada Δf = 1/(2 Tm), o un error relatiu de Δf / f = 1/(2 f Tm), on Tm és l'interval de temps, i f - la freqüència de mesurament. L'error disminueix a mesura que la freqüència augmenta, de manera que el problema és més significatiu en les freqüències baixes, on el nombre de mostres 'N' és petit.
Ús d'estroboscopis
L'ús d'un estroboscopi, dispositiu especial que genera centelleigs brillants del llum intermitent amb una temporització prèviament calibrada, permet calcular la freqüència d'objectes en vibració o amb moviments rotatoris. La font de llum es dirigeix a l'objecte en rotació, i s'augmenta o disminueix gradualment la freqüència dels raigs. Quan la freqüència de la llum estroboscòpica s'equipara amb la freqüència de rotació o vibració de l'objecte, és a dir quan un cicle complet d'oscil·lació amb retorn a la posició original es produeix en l'interval entre dos flaixos, la llum estroboscòpica sobre l'objecte sembla estacionària. A partir d'aquí, el valor obtingut de la freqüència es pot llegir amb les diferents lectures. Aquest mètode, però, té un inconvenient: si la velocitat de l'objecte (x) és igual a la llum estroboscòpica de freqüència (i), però la proporcionalitat és un nombre enter (2x, 3x, etc.), ja que l'objecte sota aquestes situacions retorna una il·luminació que sembla estàtica.
Ús de freqüencímetres
Les freqüències altes es mesuren normalment amb un freqüencímetre. És un dispositiu electrònic que avalua la freqüència d'un cert senyal repetitiu, i mostra el resultat en Hertz en una pantalla digital. Els processos cíclics que no són inherentment elèctrics (com ara, per exemple, la freqüència de rotació al voltant d'un eix, vibracions mecàniques o ones de so) poden convertir-se prèviament en un senyal elèctric (mitjançant algun tipus de transductor), i llavors tractar-lo de la forma normal. En l'actualitat, aquests dispositius són capaços d'abastar un rang de fins a 100 GHz (a la pràctica, aquesta quantitat suposa un límit pels mètodes directes de mesurament). Les freqüències més altes es mesuren mitjançant tècniques indirectes.
Tècniques indirectes de mesurament
A més dels comptadors de freqüència habituals, sovint hom mesura indirectament els senyals electromagnètics mitjançant oscil·ladors locals (és a dir, convertidors de freqüència). Si partim d'un senyal de referència conegut, i el combinem amb un mesclador de freqüència no-lineal (com ara un díode), obtenim un senyal heterodí, o alternativament s'observa una diferència de freqüència entre els dos senyals de la font. Si aquesta diferència és suficientment petita, el senyal resultant pot ser captat pel mateix comptador. En conseqüència, mitjançant aquest procés es pot estimar la diferència de la freqüència respecte al senyal conegut i, per tant, la freqüència del senyal original. Si es necessita arribar a freqüències més altes, es poden emprar successives etapes de mesclat. En l'actualitat, s'està investigant l'aplicació d'aquest mètode indirecte en els senyals a la banda de l'infraroig i l'espectre visible.
Visió intuïtiva
Diferents tipus d'ones electromagnètiques tenen diferents freqüències. Una manera de visualitzar aquest fet és imaginar-nos dos trens que viatgen a la mateixa velocitat, però els vagons d'un són més petits que els de l'altre. Si algú agafés algun objecte que no estigués en moviment, com ara un senyal de trànsit, i comptés quants vagons per segon han sobrepassat el senyal per cadascun dels trens, coneixeríem la freqüència dels vagons que es mouen per cada tren. El nombre i freqüència de vagons que sobrepassen el senyal seria diferent, perquè el tren amb els vagons més petits tindria més vagons que sobrepassarien el senyal per cada segon que en el cas del tren amb els vagons grans. Si coneixem quants vagons han sobrepassat el senyal en un segon, i si coneixem també la velocitat del tren, llavors podem calcular matemàticament la grandària de cada vagó per cadascun dels trens.
Per exemple, si el tren es mou a 10 quilòmetres per segon, i passen 10 vagons per segon, llavors cada vagó té una longitud d'un quilòmetre. Si l'altre tren també es mou a 10 quilòmetres per segon, i passen 20 vagons per segon, llavors cada vagó d'aquest tren té una longitud de mig quilòmetre. Aquest exemple il·lustra que, si es coneix la freqüència d'una ona electromagnètica, podem calcular-ne la longitud d'ona, donat que totes les ones electromagnètiques viatgen a la velocitat de la llum. Així, c=ν λ, on ν és la freqüència, λ és la longitud d'ona, i c és la velocitat de la llum. Per tant, una altra manera d'expressar la freqüència és dir que la freqüència és c / ν.
Exemples
| Banda espectral | Freqüència (Hz) |
|---|---|
| raigs gamma | > 30,0 EHz |
| raigs X | > 30,0 PHz |
ultraviolat llunyà | > 1,5 PHz |
ultraviolat proper | > 789 THz |
| llum visible | > 384 THz |
infraroig proper (NIR) | > 120 THz |
infraroig mitjà (MIR) | > 6,00 THz |
infraroig llunyà o submil·limètric (FIR) | > 300 GHz |
| microones | > 1,0 GHz |
| ràdio de freqüència ultraalta (UHF) | > 300 MHz |
| ràdio de freqüència molt alta (VHF) | > 30 MHz |
| ràdio d'ona curta | > 1,7 MHz |
| ràdio d'ona mitjana | > 650 kHz |
| ràdio d'ona llarga | > 30 kHz |
| ràdio de freqüència molt baixa (VLF) | < 30 kHz |
Radiació electromagnètica
La radiació electromagnètica es propaga en forma d'ones transportant energia. Aquest tipus de radiació inclou des de la llum visible a les ones de ràdio, passant per les microones. La llum visible que percebem amb els nostres ulls és només una petita fracció de l'espectre electromagnètic i és composta per un cert nombre de colors (violat, blau, cian, verd, groc, taronja, vermell) que corresponen a certs intervals de freqüències. A la taula de la dreta es mostren algunes freqüències de l'espectre electromagnètic, i a la de sota les freqüències dels diferents colors de la llum visible.
Color | Interval de freqüència |
|---|---|
violat | ~ 790 a 700 THz |
blau | ~ 700 a 600 THz |
cian | ~ 600 a 580 THz |
verd | ~ 580 a 530 THz |
groc | ~ 530 a 510 THz |
taronja | ~ 510 a 480 THz |
vermell | ~ 480 a 405 THz |
La radiació ultraviolada (habitualment simbolitzada com a UV) que ens arriba del Sol és un exemple comú de radiació que no és visible als nostres ulls. Tot i no ser visible, ens afecta i per això utilitzem filtres especials a les nostres ulleres de sol i cremes per protegir-nos dels seus efectes.
Una altra propietat de les ones electromagnètiques és la longitud d'ona. La longitud d'ona és inversament proporcional a la freqüència, de tal manera que les ones electromagnètiques de freqüència més alta tenen una longitud d'ona curta i viceversa. En el buit, la longitud d'ona es descriu com
- λ=c/ν{displaystyle lambda =c/nu }
on c és la velocitat de la llum. En un entorn en el qual la velocitat de la velocitat de fase sigui c' diferent de la velocitat en el buit (c' = c / n, amb n l'índex de refracció), la relació entre la longitud d'ona i la freqüència és:
- λ=cnν.{displaystyle lambda ={c over nnu }.}
Una altra característica és el nombre d'ona, que és igual al nombre de vegades que vibra una ona en una unitat de distància: k = 1 / λ. Sovint, aquest valor es multiplica pel factor 2π, per analogia amb la freqüència circular habitual, ks = 2π / λ. En el cas de l'ona electromagnètica:
- k=1/λ=nνc.{displaystyle k=1/lambda ={nnu over c}.}
- ks=2π/λ=2πnνc=nωc.{displaystyle k_{s}=2pi /lambda ={2pi nnu over c}={nomega over c}.}
So
El so és una successió de canvis de pressió en un medi (sòlid, líquid o gas), provocats per una vibració que s'hi transmet en forma d'ones sonores, que són ones mecàniques. Aquestes ones es caracteritzen també per unes freqüències que són captades per l'oïda. En el cas dels humans les freqüències audibles es troben entre els 20 i els 20.000 hertz (20 kHz), tot i que aquests límits varien de manera decreixent en augmentar l'edat, especialment per a les freqüències altes.[3] Altres espècies animals tenen altres intervals de freqüències audibles, els gossos, per exemple, poden percebre sons a freqüències superiors als 20 kHz.
Electricitat

Tensió i freqüència:
220-240 V/60 Hz
220-240 V/50 Hz
100-127 V/60 Hz
100-127 V/50 Hz
Una de les característiques que defineixen el corrent altern és la seva freqüència, a Europa, Àfrica, Austràlia, la major part d'Àsia i la part sud d'Amèrica del Sud s'utilitzen alternadors que produeixen electricitat de 50 Hz. Mentre que a Amèrica del Nord i la part nod de Sud-amèrica utilitzen una freqüència de 60 Hz. La freqüència que genera l'alternador depèn del nombre de pols i del nombre de voltes per minut.
Gairebé tots els aparells elèctrics de la llar funcionen igual de bé en xarxes amb una freqüència de 50 Hz i de 60 Hz, sempre que tinguin el mateix voltatge. A finals del segle xix i la primera meitat del segle xx, abans de la normalització, existien diverses xarxes aïllades, amb freqüències que anaven des dels 16 2⁄3 Hz fins als 133 1⁄3 Hz.
En la xarxa a bord de les aeronaus, submarins, etc. s'utilitza la freqüència de 400 Hz. Aquesta major freqüència possibilita reduir el pes i la grandària dels transformadors, encara que augmenta la pèrdua de transmissió a través de llargues distàncies.
Per determinar la freqüència del corrent altern produït per un generador elèctric, s'utilitza la següent equació:
F=P⋅Vg120{displaystyle F={Pcdot V_{g} over 120}},
on F és la freqüència (en Hz), P és el nombre de pols (sempre han de ser parells), i Vg és la velocitat de gir (en rpm).
Freqüències especials
Hi ha alguns intervals de freqüències que a causa de la seva utilització o característiques reben un nom especial:
Audiofreqüència: Es refereix al rang de freqüències de les ones sonores, de tipus mecànic, que són audibles pels humans, aquest interval va dels 20 Hz als 20.000 Hz.
Alta freqüència: El terme és àmpliament utilitzat en el camp de les telecomunicacions i es refereix a freqüències entre els 3 i els 30 MHz. En altres camps les freqüències poden diferir.
Freqüències preferents: Són un conjunt d'intervals de freqüències normalitzades definides a la norma EN ISO 266 que s'utilitzen per a mesuraments acústics i en les disposicions legals.
Rangs de freqüències
Molts sistemes es caracteritzen per el rang de freqüència a la que responen. Diversos exemples podrien ser, els instruments musicals que produeixen rangs de notes diferents, l'espectre que es divideix en diversos rangs com ara el visible, els infraroigs, els raigs X... i les emissores de ràdio, cada una ocupa un rang de freqüència determinat... El rang de freqüència d'un sistema és el rang on es considera que s'ofereix un nivell útil del senyal amb característiques de distorsió acceptables. Un llistat dels límits superior i inferior dels límits de freqüència per a un sistema no és útil sense saber què representa el rang. També es pot parlar parlar d'amplada de banda quan es fa referència al rang de freqüències d'un senyal analògic.
Referències
↑ Gmurman, V. E.. Teoriia veroiatnostei i matematicheskaia statistika Uchebnoe posobie dlia vuzov. (en rus). 11a ed.. Moscou: Vysshaia shkola, 2005. ISBN 5-06-004214-6.
↑ Bakshi, U.A.; Bakshi, A.V.. Electronic Measurement Systems (en anglès). Technical, 2009, pàg. 4-14. ISBN 9788184316032.
↑ De vegades es pren la fontera entre els sons audibles i els infrasons en els 16 Hz.
Bibliografia
Giancoli, D.C.. Physics for Scientists and Engineers (en anglès). 2a ed.. Prentice Hall, 1988. ISBN 0-13-669201-X.
Stöcker, Horst. Taschenbuch der Physik (en alemany). 4a ed.. Frankfurt am Main: Verlag Harry Deutsch, 2000. ISBN 3-8171-1628-4.
Dickreiter, Michael. Handbuch der Tonstudiotechnik (en alemany). 6a ed.. Múnic: K.G. Saur Verlag KG, 1997. ISBN 3-598-11320-X.
Vegeu també
- Amplitud
- Freqüències del piano
- Acústica musical
- Filtre electrònic
- Llindar d'audició
- Ressonància mecànica
- Domini freqüencial
| A Wikimedia Commons hi ha contingut multimèdia relatiu a: Freqüència |
![]()
Viccionari



















